Dott. Ing. Flavio Mattavelli
Metodo di Mattavelli per i
canards.
Per il calcolo delle posizioni approssimate del punto neutro.
Release settembre 2025, update
novembre 2025.
Legenda.
NP = Punto neutro (Neutral Point) dell’intero velivolo, posizione
nella quale il totale dei momenti di beccheggio è costante (nullo a CG
coincidente) al variare dell'incidenza e quindi delle portanze dell’ala e delle
alette canard.
D% = distanza
espressa in percentuali della lunghezza MAC, distanza della posizione di NP in avanti, a partire dal bordo di
entrata della MAC dell’ala posteriore (MAC idealmente da spostare
ortogonalmente sull’asse longitudinale, per valutare la posizione anche del
CG).
D% = 100 * D / MAC, essendo D = distanza espressa
in unità metriche di lunghezza.
D = D% * MAC / 100 = lunghezza della distanza dell’NP in unità di lunghezza, rispetto al
bordo di entrata della MAC proiettato sull’asse longitudinale del canard.
MAC = Mean Aerodynamic Chord, corda media aerodinamica, se senza precisazioni
intesa dell’ala posteriore. Riportare la lunghezza della MAC spostandola
idealmente ortogonalmente fino all’asse longitudinale del modello, poi usare il
bordo di entrata della MAC spostata sull’asse longitudinale come punto di
riferimento per i calcoli di D.
CG = Centro di gravità o meglio delle masse. Trovata la distanza D, consegue la
posizione del CG ideale del canard, tramite il concetto di margine statico, che
qui non viene approfondito. In breve il CG va posizionato davanti rispetto
all’NP, in una posizione che indico variabile dal 4 al 18 % MAC,
preferibilmente consiglio porre preliminarmente tale margine statico a circa
11%, da definire in pratica dopo i primi voli.
Sc =
superficie delle alette anteriori, Sw = superficie dell’ala posteriore, in unità metriche di
lunghezza ^2
P = distanza
metrica tra i centri aerodinamici di ala e alette canard, centri che sono per
convenzione posizionati ognuno al 25% della propria MAC, dietro i rispettivi
bordi di entrata.
W = coefficiente di efficacia dell’ala posteriore, in pratica stimato
convenzionalmente sempre = 0,85 (variabile però in teoria da 0, 8 a 1). W
dipende dal downwash dell’aletta anteriore e dai
profili delle ali, comunque per un aeromodellista senza pretese va bene 0,85,
come in seguito utilizzato nella formula
di equilibrio statico, riconoscibile perlopiù nella seguente espressione di
C, altrimenti detta formula di Peppe 46 nel
forum Barone Rosso, valida per ogni singolo canard.
C = Sc * P / (W * Sw + Sc) = distanza longitudinale tra il
centro aerodinamico dell’ala posteriore e l’NP del canard. Questa distanza, che
è in unità metriche di lunghezza, può essere espressa in percentuali della MAC,
cioè diviene C% = C * 100 / MAC.
Come conseguenza D% reale dovrebbe essere = C% – 25% MAC.
C non è proposta per famiglie di
canard, ma contiene parametri che, fra loro diversamente rapportati, possono
determinare diverse famiglie (per la cui definizione vedere nei Fondamentali).
K = Sc * P / Sw * MAC = rapporto volumetrico delle alette
anteriori, definito per i canards come tradizionalmente per i velivoli
convenzionali.
Fondamentali.
Il metodo riguarda soltanto la
ricerca di un D% più approssimato possibile, che sia valido con diverse
approssimazioni per tutti i canards in funzione di K, però inizialmente è basato sul calcolo di C con coefficiente di
efficacia dell’ala posteriore supposto W = 0,85.
Notare
che per canards particolarmente efficienti (cioè con W > 0,85) l’NP si
sposta indietro e la
posizione fissata del CG potrebbe essere troppo avanti, cioè si potrebbe avere
un modello forse picchiato.
In calce, nel capitolo Seguito e
conclusione, tuttavia ho analizzato anche 0,85 < W < 0,95.
A parità dei parametri P/ MAC e Sw possono volare diversi canards, a condizione che il loro
K sia compreso tra circa 0,3 e 1,25, per avere la necessaria stabilità
longitudinale.
P/MAC è solitamente compreso tra 2,5
e 5. Ciò significa che, per K = 1, il rapporto Sc/Sw
debba essere compreso tra 0,4 e 0,2.
Infatti ad es. per P/MAC = 2,5
consegue 1 = 2,5 * Sc/Sw quindi Sc/Sw = 1/2,5 = 0,4. Analogamente per P/MAC = 5 risulta Sc/Sw = 0,2 solo per K = 1.
Il rapporto Sc/Sw
varia al variare di K. Esempio per K = 0,3 il rapporto Sc/Sw
deve essere compreso tra 0,12 e 0,06, mentre per K = 1,25 lo stesso rapporto
deve essere tra 0,5 e 0,25.
Prefissando,
oltre a P & MAC, la superficie Sw,
l’unico parametro variabile è Sc, anzi è meglio intendere variabile il rapporto
Sc/Sw, per ragionare su canards in scale diverse.
Meglio anche riferire sempre
tutte le distanze geometriche alla MAC, intendendole come percentuali della MAC medesima.
Definisco famiglia di canard l’insieme dei canard aventi prefissati comuni i
parametri P/MAC e Sw in valori costanti,
caratterizzanti la famiglia, valori tutti uguali solo per i famigliari.
Ciò comporta che soltanto Sc debba
essere variabile nella stessa famiglia, al fine di ottenere lo stesso K tramite
il rapporto Sc/Sw che potrebbe caratterizzare K
diversi nella stessa famiglia.
Cioè ad ogni diverso K della stessa
famiglia di canard è associato un rapporto Sc/Sw
diverso, con valore uguale solo per qualsiasi canard della stessa famiglia
avente lo stesso K, ma rapporto Sc/Sw con valore
diverso per lo stesso K in famiglie diverse. Cioè a parità di K nelle diverse
famiglie di canard esistono rapporti Sc/Sw diversi.
Dunque ogni rapporto Sc/Sw può essere inteso come
caratterizzante una famiglia purché venga sempre associato ad un K di
riferimento. In questo senso ho chiamato le famiglie ciascuna con il nome di
Sc/Sw associato al K =1, pertanto le famiglie variano
in pratica da Sc/Sw = 0,4 a 0,2, solo per K = 1 di
riferimento.
Ogni famiglia ha una propria
disposizione dei D% dei propri canards, disposizione concretizzabile nel piano
cartesiano (K, D%) tramite una curva
caratteristica che rappresenta le posizioni D% approssimative del punto neutro
dell’intero modello, avente come connotato comune dei canards delle altre
famiglie il rapporto volumetrico K delle alette anteriori.
Occorre prefissare Sw e P/MAC per quantificare in una famiglia precisa la
variabilità di D% rispetto a Sc variabili e quindi a K diversi, ma nella stessa
famiglia di canards.
Scopo del metodo
Lo scopo è trovare una formula
(approssimativa) valida
per (quasi) tutti i canard, che permetta di trovare direttamente e rapidamente,
a W noto, la distanza D% in base soltanto alla conoscenza dei K, con K
variabili per (quasi) tutti i diversi canard possibili, tollerando gli errori
dei D accettabili nella maggioranza dei casi.
In Seguito e conclusione è stato poi
fatto un ulteriore passo per ipotizzare la curva D% anche con W ignoto.
Riassunto del procedimento.
In realtà per ogni singolo canard una
formula per il calcolo del D% esiste già, è la formula detta di Peppe 46 nel
forum Barone Rosso, cioè la distanza C =
Sc * P / (W * Sw + Sc).
Da questa formula si può ricavare una
distanza C% in percentuale MAC e poi un D% (comunque presunto) reale
ricalcolando D% reale = C% – 25% MAC, tuttavia
ciò vale per un solo canard e solo per quel K corrispondente a un certo valore
di Sc/Sw, perchè la formula
di Peppe 46 non si riferisce ad alcun K.
In un piano cartesiano assumere come
asse delle ascisse K, mentre porre in ordinata D%.
Primo esempio denominato poi B% (curva rossa, per dettagli
vedere avanti la Storia dettagliata).
Dapprima
ho acquisito alcuni valori (supposti) reali di D% utilizzando la formula di
Peppe 46 con W = 0,85.
Poi ho
tabulato i diversi D% reali in base ai diversi Sc, cioè ai diversi K, per
trovare una curva per punti reali, valida per tutti i canard di una famiglia,
quella avente Sc/Sw = 0,4 con K = 1, curva che è
stata da me approssimata in un primo tempo dalla (quasi) “retta” D% = 65 K – 10
* (radice quadrata di K), formula oggi
erronea, ma proposta nel forum Barone Rosso, discussione Rapporto volumetrico dei
canard, post #29. C’è un esempio di
calcolo nella seguente immagine n° 01.
Questa
formula è erronea soltanto per un uso generale per tutti i diversi canards
pensabili, mentre è precisamente ben valida soltanto nella fattispecie del
canard analizzato, siccome per esso si ritiene proprio vero che W = 0,85.
Quando
invece si considera un altro canard, del quale non si conosce il W, tale
formula può divenire sbagliata, in generale per tutti i diversi canards
pensabili, con diverse prerogative specifiche, avendo caratteristiche di
famiglie diverse.
Comunque
l’equazione della formula suddetta, o della sua (quasi) “retta”, è accettabile
solo per 0,75 < K < 1, non vale per tutti i canard possibili, in quanto altre famiglie hanno curve
diverse, pur con andamenti tutti simili, assimilabili tutti a vere parabole, ma
con rami quasi totalmente rettilinei, solo malamente assimilabili a rette, solo
in una ristretta zona del campo cartesiano.
Invece la giusta curva è stata poi
individuata e tabulata come esempio B% (parabola rossa).
Come secondo esempio, denominato poi A% (curva verde scuro), ho
ricavato i punti per la famiglia Sc/Sw = 0,2 con K =
1, intendendola opposta agli estremi del primo esempio, a sua volta inteso come
estremo, disegnando le 2 curve così
dette estreme di un campo comprendente (quasi) tutti i canard possibili, sempre con W = 0,85.
Potrebbero
esistere altri canards all’esterno dei confini di tale campo, cioè i 2 esempi
fatti limitano un campo ristretto, ma utile per valutare gli errori di
approssimazione della maggioranza dei canards, maggioranza stimata tutta
all’interno del suddetto campo tra A% & B%, con errori calcolabili ai
confini del campo. All’esterno del campo eventuali improbabili canards avranno
errori ovviamente maggiori di quelli calcolati.
Allora ho cercato una curva intermedia alle due estreme,
intermedia che vale quindi per (quasi) tutti i canards, con la massima
approssimazione possibile, cioè con minimi errori rispetto ai valori reali del
canard che vogliamo studiare, non più con la formula di Peppe 46, bensì tramite
una mia nuova formula che offrirà valori
di D% della curva intermedia, quindi non reali ma ipotetici, in funzione
dei K reali. Rispetto ai D% ipotizzati dalla formula i D% reali avranno errori
di approssimazione accettabili senza dover ricalcolare ogni volta la distanza C.
Siccome si tratta di una formula polivalente, utilizzante
diversi parametri della definizione dei K di varie famiglie, se non volete
ricalcolare ogni volta la Vs. curva specifica della singola famiglia del Vs.
canard, potete fare riferimento diretto alla curva intermedia, scoperta e
proposta più avanti tramite l’equazione di una parabola. Dopo il calcolo con il Vs. K vi troverete nel
Vs. canard con errori minimi di D% e perciò accettabili nella maggioranza dei
casi.
La curva ipotetica intermedia tra le parabole A% & B% è stata denominata Y%
(curva nera) ed è stata
tabulata in calce al presente articolo, nelle 2 tabelle che ricapitolano anche gli errori
di approssimazione di Y rispetto A & B, validi solo con W = 0,85 (*).
Poi
vedere anche Seguito e conclusione per 0,85 < W < 0,95.
Storia dettagliata
Esistono infinite rette che
potrebbero approssimare, una per una, le varie curve specifiche di ogni
famiglia. Il fascio di rette però non ha un centro comune e la situazione non
sarebbe rappresentabile con un’unica retta intermedia che abbia quasi gli
stessi errori in tutti i punti, rispetto a 2 curve estreme di 2 famiglie
estreme.
Rette intermedie assimilanti inefficaci.
In un primo tempo avevo erroneamente
pensato che fosse possibile trovare una sola retta, intermedia a tutto il
fascio di rette, che approssimasse l’andamento della curva intermedia tra le
curve estreme, ai limiti di tutte le possibili famiglie, ma tale idea si è
dimostrata in parte inefficace.
Comunque, considerando che anche una
curva intermedia sarebbe approssimabile in parte da una retta per un tratto
intermedio, si può comunque ragionare sulle sole rette.
Dapprima avevo erroneamente pensato
di approssimare la curva intermedia con l’equazione D% = 72,5 K – 10 * (radice
quadrata di K) = 62,5% per K = 1, perché per le curve ai confini B% & A%
avevo stimato rispettivamente 55% e 70% circa per K = 1.
Poi però ho pensato fosse meglio
ricorrere alla vera retta D% = 72,5 K – 10 = 62,5% senza moltiplicare la radice
quadrata di K, per K = 1, ma anche così l’approssimazione non è buona.
Forse, se proprio si volesse
perseverare per cercare una retta approssimante più casi possibili, con minori
approssimazioni e maggiori errori della distanza D% in alcuni casi, si potrebbe
utilizzare meglio la seguente formula per la retta intermedia più semplice possibile. Osservando le 2 curve
tracciate su un disegno cartesiano, ho individuato la retta avente D% = 62,5%
per K = 1, inoltre D% = 24% per K = 0,5, cioè si potrebbe accettare, da K = 0,5
fino a 1,25, l’equazione della retta D%
= 77% K – 14,5%, retta comunque inefficace rispetto all’equazione della
parabola intermedia che verrà trovata più avanti. E’ quindi meglio abbandonare l’idea di rette intermedie assimilanti, in
quanto verranno meglio sostituite dall’equazione proprio di una parabola
intermedia valida, cioè Y%.
Dettagli primo esempio (B), posto al confine inferiore del campo cartesiano analizzato.
Già nel post # 29 del
forum Barone Rosso avevo malamente proposto la formula, detta di Mattavelli, in parte errata, equazione parametrica D% = 65 * K – 10 * (radice quadrata di K) condizionata dai K della
stessa famiglia. Tale formula è buona solo per un ramo di curva quasi retto e
soltanto per una famiglia di canard, precisamente quella per la quale Sc / Sw = 0,4 per K = 1, con costanti P/MAC = 2,5 e W = 0,85. La
(radice quadrata di K) moltiplicante il secondo fattore era proposta per ottenere una quasi retta quasi
coincidente con la curva dei D% solamente tra K = 0,75 e K = 1, in un tratto
dove cioè l’errore di approssimazione è praticamente sempre nullo, ma
aumentando gli errori di approssimazione negli altri tratti della parabola B% =
esatta curva D%.
In realtà impiegando la radice
quadrata di K si realizza una parabola con il ramo interessante quasi
rettilineo, ma di leggerissima concavità comunque minore della reale, dunque è uno sfizio superfluo moltiplicare
la radice quadrata di K, anzi in pratica sarebbe meglio non moltiplicarla
affatto, scrivendo solo D% = 65 K – 10,
che è una vera retta, con diverse approssimazioni, ma pur accettabile solo per
tratti della reale curva B%. La retta D% = 65 K -10 sarebbe (poco) meno
approssimata alla suddetta famiglia di canards B% per valori K < 1, però
ritroverebbe la curva reale per circa K = 0,5 e quindi sarebbe (poco) più
approssimata per i K < 0,5.
Di formule simili alla precedente se
ne potrebbero scrivere tante altre.
Per altri diversi canards
bisognerebbe comunque ricalcolare le singole curve famigliari e trovare altre
rette che approssimino meglio ogni singola curva, se si volesse insistere con
l’idea delle rette di confine del campo B & A assimilanti le reali curve
D%, idea che consiglio ancora di
accantonare del tutto.
Invero la curva B% sarebbe meglio
approssimata dalla D% = 65 K + 20 *
(radice quadrata di K) - 30, ma quest'ultima equazione non è una retta, sembrerebbe
una parabola “inversa”, ma non è la parabola esatta B%, che si vedrà è quasi
rappresentabile dall’equazione D% = - 20
K^2 + 95 K – 20, tuttavia meglio ancora dalla D% = - 21 * K^2 + 98 * K – 22 (vedere Precisazioni su A% & B%).
La vera curva B% è difficile da
trovare, ma non impossibile, anzi diviene facile,
come si vedrà più avanti, impiegando un calcolatore di parabole on-line.
Dettagli secondo esempio (A), posto al confine superiore del campo cartesiano analizzato.
Volendo perseverare con le
approssimazioni rettilinee, anche la seguente formula potrebbe essere
accettabile, nel senso di essere però meno approssimata in alcuni casi e più
approssimata per altri casi di K. Alludo alla retta D% = 85 K – 15.
Questa è una retta che approssima la
curva A% nel piano cartesiano, ricavabile per Sc/Sw =
0,2 con K = 1, dopo aver prefissato P/MAC = 5 e Sw =
40 (unità di lunghezza ^2), sempre con W = 0,85, per una diversa famiglia di
canards, ritenibile in una posizione estrema, opposta al caso B, allo scopo di
cercare poi una curva intermedia Y% del campo analizzabile tra A & B.
L’esempio A corrisponde ad un canard
che avevo già introdotto nel post #26,
successivamente abbandonato, perché avevo allora accantonato l’idea di
utilizzare gli allungamenti alari, o meglio solo l’allungamento dell’aletta
anteriore ARc, a favore dell’utilizzo del solo K per
la formula del D%. Solo ARc verrà usato nel Seguito e
conclusione di quest’articolo.
L’equazione D% = 85 K – 15 comunque approssima
molto bene la curva A% in analisi, quindi si potrebbe quasi non cercare la
parabola rappresentativa, ma utilizzare subito detta retta per acquisire i D%
della sola curva A%.
Curva intermedia (Y% nera).
Gli esempi A & B possono
rappresentare i limiti di un campo di due casi estremi di canards possibili,
quindi un'ulteriore curva, definita
intermedia Y%, giacente in mezzo a tale campo rappresenterebbe un canard, denominabile "standard"
di riferimento, rispetto al quale si possono valutare correttamente le
discrepanze dei D% dei canards specifici.
Tale curva intermedia è dunque
situabile a metà tra la curva B% intesa con Sc/Sw =
0,4 per K =1 e l'altra curva A%, disegnabile più in alto di B% nel piano
cartesiano, intesa con Sc/Sw = 0,2 per K =1, entrambe
da intendersi con anche P/MAC diversi fra loro, ma costanti prefissati, con
diversi Sw prefissati, per le 2 famiglie estreme del
campo di tutti i canards possibili.
Si potrebbe discutere sulla validità
della scelta delle 2 famiglie estreme A & B, poste da me ai confini del
campo, però per me non serve.
Piuttosto, fondamentalmente tutti i casi possibili di D% sono risultati in
pratica giacenti su curve assimilabili a parabole strutturate con K diversi,
forse parabole “inverse” (con radice dell’ascissa cartesiana K), o altro genere
di curve, ma anche sono identificabili in parabole tradizionali (con K^2
nell’equazione), ai fini dello studio dei tratti di curva che ci interessano.
Cercando la curva intermedia al campo
analizzato, ho trovato per caso quasi valida l’equazione D% = 65 K + 24 * (radice di K) – 27, che credo sia appunto una
parabola inversa, però non mi pare una parabola tradizionale acquisibile da un
calcolatore on line partendo da 3 punti noti.
Comunque l’ultima equazione è assai
approssimata, ma non è esatta come la parabola intermedia denominata Y% nelle
tabelle ed acquisita con un calcolatore on line.
Contrariamente alle mie impressioni
iniziali, le parabole in questione possono essere analizzate ad assi verticali
e vengono utilizzati solo i rami di sinistra scendenti in basso delle parabole,
che hanno il vertice in alto. Io dapprima pensavo che le parabole fossero
“inverse” ad asse orizzontale con vertice a sinistra ed utilizzassimo solo i
rami alti risalenti a destra, pensando di usare la radice quadrata di
K…occorrerebbe invertire la funzione D%, ma ho perso i ricordi di matematica.
Procedimento ritenibile esatto
Nella maggioranza dei canards il
rapporto Sc/Sw varia da famiglia a famiglia a parità
di K, es. diciamo varia da circa 0,4 (caso B) fino a circa 0,2 (caso A) per K =
1.
Ripeto che in pratica tutte le
famiglie di canard esistenti hanno parametri compresi tra i 2 casi estremi A
& B citati. Ho pensato di trovare una curva di parabola ad andamento
intermedio tra i 2 casi estremi, in modo tale che, in qualsiasi situazione di
qualsivoglia canard, si possa individuare una distanza ideale D% = Y% rispetto
alla quale il valore reale D% del Vs. canard possa presentare un errore di
calcolo minimo, cioè un’approssimazione massima possibile.
Apparentemente sembrava un problema
insormontabile, invece fortunatamente in Internet esistono calcolatori
dell’equazione di qualsiasi parabola noti 3 suoi punti di passaggio.
Dopo aver disegnato per punti,
ricavati tramite C, le curve paraboliche dei 2 casi estremi ed individuato 3 punti
di passaggio della parabola intermedia, tramite un calcolatore on line ecco
dunque una formula della parabola
intermedia Y%, approssimativa, ma valida per (quasi) qual si voglia modello
canard, per la posizione del suo punto neutro NP, posizione data come distanza
in percentuale della lunghezza della MAC alare, in avanti rispetto al bordo di
entrata della medesima MAC.
D% = - 21,2 * K^2 + 109,7 * K – 26 arrotondabile in D% = Y % = – 21 * K^2
+ 110 * K – 26.
In realtà anche questa formula è perfezionabile. Dopo aver provato un po’ di conteggi,
è meglio usare altre formule simili, anzi ho fissato l’attenzione sulla
parabola intermedia arrotondata qui definitiva Y% = – 18*K^2 + 103
*K – 22, anche se penso che ogni altra parabola avente coefficienti
intermedi a quelli scritti nelle 2 parabole Y % sopra indicate potrebbe andare
bene. Eventuali discrepanze dovrebbero essere trascurabili, soprattutto ai
bassi K, dove (quasi) tutte le parabole in questione convergono.
Ho
realizzato 2 tabelle riassuntive degli
esempi B & A, intese ognuna ai confini del campo di possibile esistenza
di (quasi) tutti i canards da analizzare (*).
Precisazioni sulle equazioni delle parabole A% & B%.
Riporto le equazioni dei 2 casi estremi, visti come parabole
passanti per 3 punti noti dai valori di K e D% (supposti) reali quando
calcolati tramite C, con D% = C% - 25% MAC.
Notare che le 3 curve a parabola A, B
e Y analizzate non hanno affatto lo stesso vertice!
B) curva [rossa] del primo esempio Sc/Sw
= 0,4 per K = 1
Posti i punti K = 1.25 con D% =67.5,
K = 1 con D% = 55, K = 0,5 con D% = 22,5 risulterebbe la parabola D% = - 20 K^2 + 95 K – 20. Quindi per K
= 0,75 risulta D% = - 11,25 + 71,25 – 20 = 40 % mentre per K = 0,3 risulta D% =
-1,8 + 28,5 – 20 = 6,7 %. Tuttavia i 3 punti di partenza, presi su di un
grafico grossolano, non corrispondevano bene, allora poi la curva B è stata
ricalcolata, migliorata in tabella con la B% = - 21 K^2 + 98 K –
22, con valori diversi.
A) curva [verde scuro] del secondo esempio Sc/Sw = 0,2 per K = 1
Posti i punti K = 1.25 con D% =88.5,
K = 1 con D% = 70, K = 0.5 con D% = 27.5 risulta, sempre tramite calcolatore on
line, la parabola A% = - 16 K^2 +
110 K – 24. Quindi per K = 0,75 risulta A% = - 9 + 82,5 – 24 = 49,5
%, mentre per K = 0,3 risulta A% = – 1,44 + 33 – 24 = 7,56 %.
Errori di approssimazione in % MAC.
Calcolato il D% dalla formula della
parabola intermedia Y%, esso, rispetto al D% reale, in percentuali MAC,
dovrebbe avere un errore circa + o - 7,5% per K = 1 nei casi estremi di canards
reali ai confini del campo, ma l’errore potrebbe essere sempre nullo per ogni K
qualora il canard reale avesse i parametri corrispondenti alla famiglia della
parabola intermedia Y%, cioè con Sc/Sw = 0,3 e P/MAC
= 3,75 circa.
L’errore diverrebbe maggiore di + o –
7,5% per K > 1 fino all’errore massimo circa + o - 11% per K < 1,25,
mentre potrebbe esserci un errore sempre in diminuzione tra circa + o - 3% e 1%
nei 2 casi estremi per K < 0,5, fino al minimo valore utile di K = 0,3.
Per tutti i possibili casi di qualsiasi canard intermedio avente K
compreso tra K = 0,5 e K = 1, che sono i valori
di K più comuni, l’errore dovrebbe risultare compreso in crescendo dal suddetto
circa + o - 3% fino al + o – circa 7,5% massimo, sempre in percentuali MAC.
Si tratta di errori per me accettabili per la maggioranza degli
aeromodelli canard,
comunque credo ben minori dell’errore rientrante intrinsecamente nell’aleatorietà
della scelta fatta imponendo il coefficiente W = 0,85.
Casi per W > 0,85.
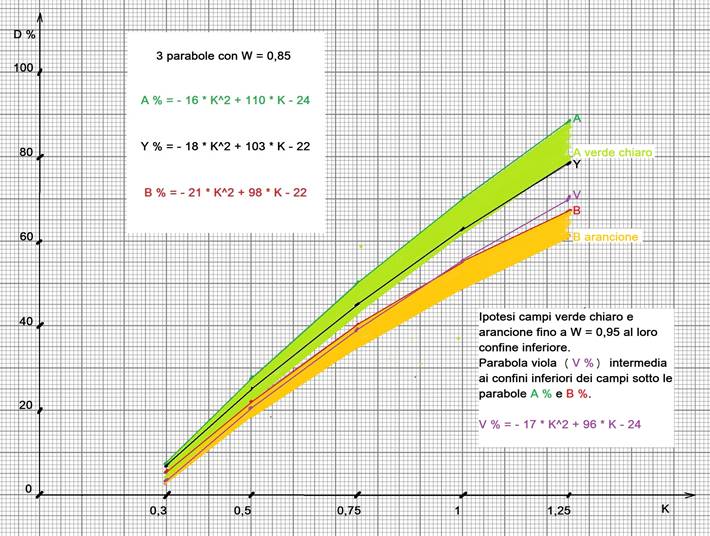
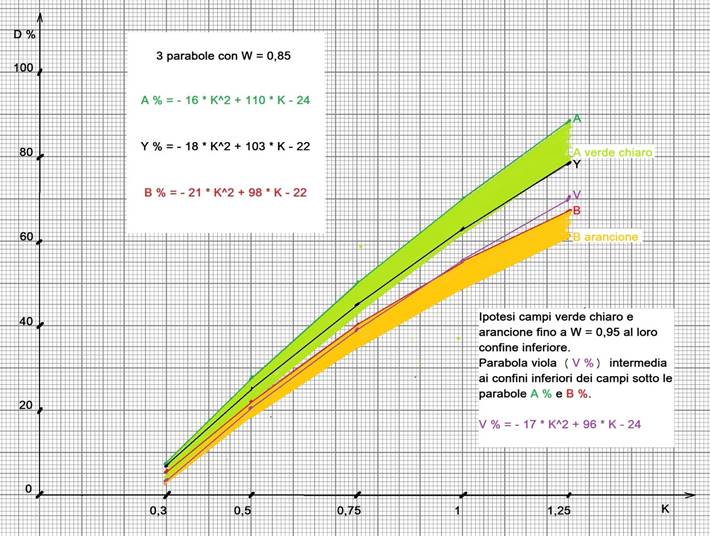
Nel grafico ho tracciato anche le curve verde chiaro e arancione,
corrispondenti ai casi alternativi di A (verde scuro) e alternativo di B (rosso),
qualora entrambi con coefficiente W = 0,95.
In tali casi l’NP si sposta
indietro con D% rispettivamente più bassi.
Ovviamente la parabola Y% sarebbe
eccessivamente in alto e non più intermedia, qualora il canard da analizzare si
trovasse ai confini inferiori dei campi colorati, sulle curve verde chiaro
oppure arancione. In tali casi il canard A verde chiaro con W = 0,95 sarebbe
ben rappresentato proprio dalla parabola Y% nera, mentre il canard B arancione
con W = 0,95 avrebbe errori di approssimazione alla Y% nera assolutamente
inaccettabili. Per W >
0,85 segue dopo le prime 2 tabelle.
================================================================
(*) Nelle
prime due tabelle la differenza (A – Y) è l’errore massimo di approssimazione %
di un canard posto al confine superiore A % del campo studiato, mentre (Y – B)
è l’errore massimo di approssimazione % di un canard posto al confine inferiore
B % del campo studiato.
Il campo studiato è solo tra le
parabole A% e B%.
|
Esempio A di
canard al confine superiore del campo
intermedio tra A & B |
K = Sc * P /
Sw * MAC |
|||||||
|
P = 10 lung. |
MAC = 2 lung. |
Sw = 40 lung.^2 |
W =0,85 |
Parabola intermedia Y% = – 18*K^2 + 103 *K – 22 |
||||
|
P/MAC = 5 |
W * Sw =
34 |
D% conf. superiore = A% = – 16*K^2 + 110*K – 24 |
||||||
|
C = Sc *P / (W*Sw
+ Sc) |
C% = C*100 / MAC |
D% reale = C% – 25% |
||||||
|
K |
Sc |
Sc/Sw |
C |
C% |
D%reale |
A % |
Y % |
A – Y |
|
1,25 |
10 |
0,25 |
2,27 |
113,5 |
88,5 |
88,5 |
78,62 |
9,88 |
|
1 |
8 |
0,2 |
1,9 |
95 |
70 |
70 |
63 |
7 |
|
0,75 |
6 |
0,15 |
1,5 |
75 |
50 |
49,5 |
45,12 |
4,38 |
|
0,5 |
4 |
0,1 |
1,05 |
52,5 |
27,5 |
27,5 |
25 |
2,5 |
|
0,3 |
2,4 |
0,06 |
0,66 |
33 |
8 |
7,56 |
7,28 |
0,28 |
|
Esempio B di canard
al confine inferiore del campo intermedio tra A & B |
K = Sc * P /
Sw * MAC |
|||||||
|
P
= 10 lung. |
MAC
= 4 lung. |
Sw = 72 lung.^2 |
W =0,85 |
Parabola intermedia Y% = – 18*K^2 + 103 *K – 22 |
||||
|
P/MAC
= 2,5 |
W * Sw = 61,2 |
D% conf. inferiore = B% = – 21*K^2 + 98*K – 22 |
||||||
|
C
= Sc *P / (W*Sw + Sc) |
C%
= C*100 / MAC |
D%
reale = C% – 25% |
||||||
|
K |
Sc |
Sc/Sw |
C |
C% |
D%reale |
B % |
Y % |
Y
– B |
|
1,25 |
36 |
0,5 |
3,703 |
92,57 |
67,57 |
67,68 |
78,62 |
10,94 |
|
1 |
28,8 |
0,4 |
3,2 |
80 |
55 |
55 |
63 |
8 |
|
0,75 |
21,6 |
0,3 |
2,6 |
65 |
40 |
39,68 |
45,12 |
5,44 |
|
0,5 |
14,4 |
0,2 |
1,904 |
47,6 |
22,6 |
21,75 |
25 |
3,25 |
|
0,3 |
8,64 |
0,12 |
1,237 |
30,75 |
5,75 |
5,51 |
7,28 |
1,77 |
Aggiungo per completezza anche alcuni
dati inerenti le curve limite A verde chiaro e B arancione,
entrambe da intendersi esclusivamente con W = 0,95.
C = Sc *P / (W*Sw
+ Sc) determina C% e poi A% verde chiaro, oppure B% arancione, entrambe curve
per punti delle posizioni D% reali ai confini di un nuovo campo di canards più
efficienti del solito, essendo W = 0,95, secondo i valori impostati di Sc
variabili con K, con prefissati P/MAC diversi e Sw
diverse.
Sc, P/MAC e Sw
sono però gli stessi delle tabelle precedenti, cioè è come se la curva A% verde
scuro fosse trasferita idealmente in quella A% verde chiaro e la curva B% rossa
fosse trasferita idealmente in quella B% arancione, coprendo nel trasferimento
i rispettivi campi colorati in verde chiaro ed arancione, siccome i C ed i C%
dell’ultima tabella sono mutati.
|
P = 10 lungh. |
MAC = 2 lung. |
Sw = 40 lung.^2 W*Sw = 38 |
W = 0,95 |
MAC
= 4 lung. |
Sw = 72 lung^2 W*Sw = 68,4 |
W = 0,95 |
|||
|
!!!!!!!!!! |
Calcolo della curva A% verde chiaro |
Calcolo della curva B% arancione |
|||||||
|
K |
Sc |
C |
C% |
A% ve. |
Sc |
C |
C% |
B% ar. |
|
|
1,25 |
10 |
2,08 |
104 |
79 |
36 |
3,44 |
86 |
61 |
|
|
1 |
8 |
1,739 |
86,95 |
62 |
28,8 |
2,96 |
74 |
49 |
|
|
0,75 |
6 |
1,36 |
68 |
43 |
21,6 |
2,4 |
60 |
35 |
|
|
0,5 |
4 |
0,95 |
47,5 |
22,5 |
14,4 |
1,739 |
43,47 |
18,47 |
|
|
0,3 |
2,4 |
0,59 |
29,5 |
4,5 |
8,64 |
1,122 |
28 |
3 |
|
Se si stimasse che il Vs. canard B arancione
abbia W= 0,95 si potrebbe considerare come parabola intermedia, utile ai fini
dell’approssimazione della posizione D% reale del B arancione, la parabola
rossa B% ora intesa come fittizia, ma utile per calcolare una posizione
approssimativa del punto neutro NP senza calcolare C.
In un approccio più preciso tuttavia
la vera curva intermedia
tra i confini inferiori dei campi verde chiaro ed arancione è
quantificabile nella parabola viola V% = - 17 * K^2 +
96 * K – 24 da impiegarsi esclusivamente
quando il coefficiente di efficacia dell’ala posteriore fosse W = 0,95.
I campi colorati verde chiaro e
arancione sono quelli dei W variabili ognuno tra 0, 85 e 0,95, rispettivamente
partendo dalle curve A% e B% (entrambe con W = 0, 85) e scendendo giù fino alle
curve A% verde chiaro e B% arancione (entrambe con W = 0,95).
Per ora non conosco un modo pratico
di conoscere l’esatto W e quindi l’esatta parabola da usarsi per il Vs. canard,
che probabilmente è con un W intermedio, però usando la parabola intermedia
viola (V%) avrete l’approssimazione migliore soltanto quando W = 0,95.
Tutti i casi intermedi tra 0,85 e 0,95 sono meglio valutabili usando
parabole intermedie tra la nera (Y%) e la viola (V%).
Però, se si valutassero tramite un’ulteriore generica parabola
intermedia situabile matematicamente tra la Y% e la V% solo in base K si
potrebbero avere errori troppo elevati di approssimazione dei D%, in base al
solo K, senza conoscere W.
Per fissare una parabola intermedia sempre ben approssimabile occorre
invece conoscere l’esatto W, o qual cos’altro che permetta di quantificare i
suoi effetti.
Noto il nuovo W si potrebbe
ricalcolare le C% delle parabole A% e B% spostate nel piano cartesiano e
trovare una nuova veramente valida parabola intermedia, valida però solo per il
nuovo W specifico prefissato, parabola che possa poi direttamente dare buoni
risultati approssimati dei vari D% sulla base dei soli K mutati a piacere,
senza ricalcolare ogni volta le distanze C, risultati buoni per ogni canard del
campo compreso tra le nuove curve A% e B% intese spostate in giù nel grafico,
con il nuovo W intermedio tra 0,85 e 0,95.
Seguito e conclusione.
Tutti bei ragionamenti, direte Voi,
ma come si può fare allora per un W intermedio?
C’è qualche alternativa con gli
stessi effetti del W intermedio, alternativa che possa essere impiegata tramite
una semplice formula, subito, senza fare troppi calcoli preliminari,
alternativa valida per qualsiasi canard studiabile nel campo in analisi, allo
scopo di determinare un D% ben approssimato?
Ho
ripreso il concetto dell’allungamento dell’aletta
anteriore canard ARc (Aspect
Ratio), che avevo in un
primo tempo accantonato, unitamente alla sua radice quarta, che era un trucco per calcolare la posizione del punto neutro
NP dei velivoli convenzionali, dove però si trattava esclusivamente
di ARw = allungamento alare anteriore, ala che qui
invece è posteriore.
Anche il downwash
dell’aletta anteriore può determinare il W, o meglio esserne una causa quasi del tutto utile nel caso dei canards.
Quindi ho associato la radice quarta
di ARc, che matematicamente ha un campo di
variabilità abbastanza limitato, quasi nello stesso rapporto degli estremi del
campo dei W, quindi quasi proporzionalmente simile, quindi ho associato detta
radice al campo di variabilità intermedio tra Y% e V%. Dopo un po’ di voli
pindarici ne è uscita l’equazione biparametrica seguente,
cioè in funzione dei solo 2 prefissati parametri K e ARc:
D% = (radice quarta di ARc) * (–
10 * K^2 + 65 * K) – 21.
Questa è un’espressione valida
approssimativamente per ogni canard con 0,85 < W < 0,95, assolutamente senza conoscere W.
Gli errori di approssimazione usando
la suddetta espressione risultano variabili, ma perlopiù piccoli ed accettabili.
La soluzione dell’equazione fa porre
il canard perlopiù intermedio o nel campo verde chiaro o nel campo arancione a
seconda del valore di ARc con gli stessi K, qualora
il canard abbia W compreso tra 0,85 e 0,95 e qualora i valori di ARc considerati siano perlopiù circa 6 oppure 3, valori che
sono stati considerati come casi di riferimento estremo per l’allungamento
dell’aletta anteriore della maggioranza dei canard esemplificati.
Precisazioni sul grafico precedente.
I canard possono assumere anche ARc intermedi tra 6 e 3 ed assumere ARc
anche (poco) maggiori o minori di questi estremi, dunque nel piano cartesiano
viene coperto tutto il campo dei D% tra A% verde
scuro e B% arancione, ma il campo di
esistenza dei canard analizzati con W = 0,85 rimane solo quello compreso tra le curve A% e B% e solo
così con curva intermedia utile per l’approssimazione Y%.
Le curve A%
e B% nel grafico sono state trasferite
idealmente ai confini inferiori dei campi colorati, rispettivamente in A% verde chiaro e B% arancione, con curva intermedia utile per
l’approssimazione V% viola, soltanto quando W = 0,95. Nel
trasferimento ideale anche la curva Y% (nera media con W = 0,85) va trasferita
in V% (viola media con W = 0,95).
Ricapitolando tutte le formule ben
approssimate.
Conoscendo K, ma se non si conosce W
e C, in generale, per trovare subito D% (e quindi la distanza del CG dal bordo
di entrata della MAC ortogonalizzata sull’asse
longitudinale, distanza CG% = D% + circa 10% in avanti) consiglio procedere nei
seguenti modi.
Se non si conosce ARc
e si ha fretta:
· Supponendo circa W = 0,85 usare la
formula D% = Y% = – 18 * K^2 + 103 * K –
22
· Supponendo circa W = 0,95 usare la
formula D% =
V% = – 17 * K^2 + 96 * K – 24
Però quasi sempre è meglio (v.
Osservazione):
· Per
qualsiasi 0,85 < W < 0,95 usare la formula
“blu” intermedia omnicomprensiva che segue, valida in tutti i campi del precedente grafico
cartesiano (K, D%):
D% = (radice quarta di ARc) * (– 10 * K^2 + 65 * K) – 21.
essendo ARc = allungamento dell’aletta
anteriore canard, di solito circa 3 < ARc < 6.
W = 0,90
nella formula “blu” è stato fatto corrispondere a circa ARc
= 4,5.
Esempio per K = 1 dalla formula “blu” con ARc
= 4,5 risulta D% = 59 %, lo stesso risultato della media tra i risultati di Y%
e V%, che sono rispettivamente 63% e 55%, notando che i coefficienti delle
parabole esatte sono stati arrotondati per facilitare i calcoli.
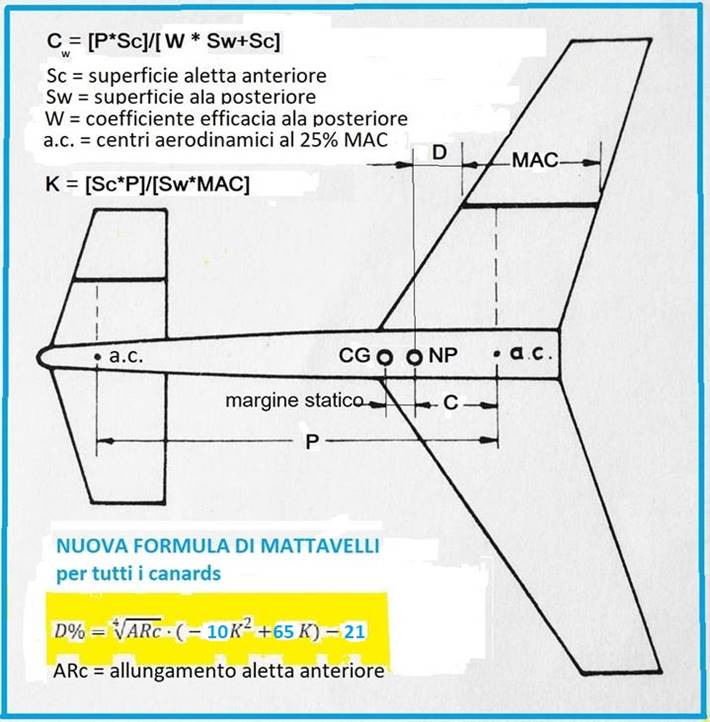
Osservazione
La nuova formula del D% nell’immagine
sopra esposta è in generale approssimativamente valida per la maggioranza dei
canards pensabili, tuttavia in alcuni casi specifici qualche altra formula tra
quelle esposte può fornire un risultato migliore, nel senso di meno
approssimativo, addirittura esatto (nei casi delle curve A% oppure B% per
W = 0,85), ma risultato valido solo per quel caso specifico.
S’intenda che la formula “blu”, oltre
a un K, ha solo un ARc caratteristico, ma tale ARc da solo, pur associato al K ideale, non è sempre
sufficientemente determinante per il risultato esatto.
Ritengo che l’allungamento
dell’aletta ARc sia comunque preponderante nel
risultato, mentre l’allungamento dell’ala posteriore ARw
potrebbe essere trascurabile (ed è stato trascurato).
Altre caratteristiche (es. profili e
incidenze, anteriori e posteriori), purtroppo non facilmente conteggiabili in
dati aerodinamici, influenzano inoltre, talora pesantemente, il coefficiente W,
e quindi determinano nascostamente la distanza D% esatta, per cui occorre
sempre considerare che la nuova formula
“blu” produce solo un’approssimazione sulla reale posizione del NP.
Flavio Mattavelli